Números decimales
- 1.- Introducción
- 2.- Comprender la parte decimal de los números
- 3.- Ubicación en el cartel de valor
- 4.- Suma de números decimales
- 5.- Resta de números decimales
- 6.- Multiplicación de números decimales
- 7.- División de números decimales
- 8.- Estrategias de cálculo mental
- 9.- Fracciones y números decimales
Los números decimales, como el resto de los conjuntos de números, tienen sus propias peculiaridades y reglas que veremos a lo largo del texto. Sin embargo, antes de ponernos a analizarlos, te brindamos la oportunidad de que descubras cuánto sabes sobre ellos con el siguiente cuestionario.
Probablemente ya conoces los números naturales (1, 2, 3, 4, 5, 6, 7, 8, …), también llamados números enteros positivos, que se usan para contar, numerar objetos y asignar posiciones, etc. Estos números son muy utilizados por las personas en la cotidianidad de la casa, la escuela, el trabajo, entre otros contextos.
Además de los números naturales, dentro de los diferentes conjuntos numéricos que existen se encuentran los llamados números decimales, que representan cantidades no enteras. Es decir, que representan cantidades menores que la unidad o mayores que la unidad pero no son unidades enteras.

Echa un vistazo a esto: Números romanos.
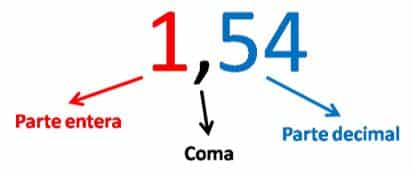
Como ves, esta persona no mide 2 metros completos, pero mide más de un metro. Este número (1,54) no representa unidades completas y es mayor que una unidad. Este número es un número decimal.
También existen números decimales menores que la unidad, como por ejemplo la altura de los pies a la cintura de esta persona, que es de 0,85 m. En este caso es un número decimal que representa menos que una unidad entera.
En el número del ejemplo anterior es posible identificar las partes del número decimal:
Utiliza las fichas que te presentamos para comprobar si manejas con soltura lo expuesto en la presentación de estos números.
Comprender la parte decimal de estos números
Para entender mejor cómo se leen y cómo se escriben los números decimales debemos comprender qué son las décimas, las centésimas y las milésimas.
Las décimas
| Tomemos una unidad: | Y ahora dividámosla en 10 partes iguales, que llamaremos décimas: |
 |
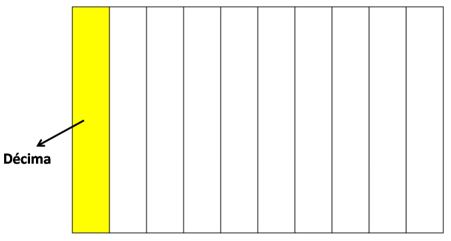 |
Como ves, una unidad se puede dividir en 10 décimas. Una décima, obviamente, es menor que una unidad. Esto quiere decir que:
Las centésimas
| Tomemos la misma unidad: | Y ahora la dividimos en 100 partes iguales, que llamaremos centésimas: |
 |
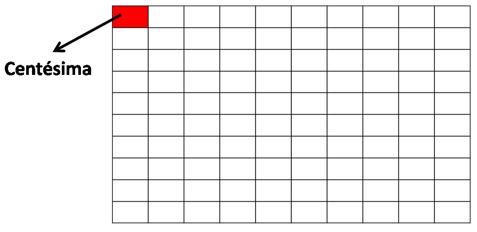 |
Aquí vemos que es posible dividir una unidad en 100 centésimas. Una centésima es mucho menor que una unidad. Esto quiere decir que:
Equivalencias entre décimas y centésimas
Si te fijas bien, puedes notar que en una décima a su vez hay 10 centésimas:
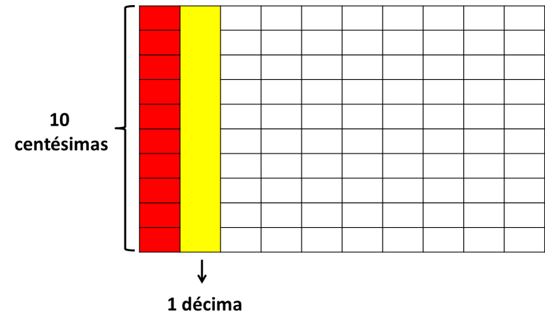
Las milésimas
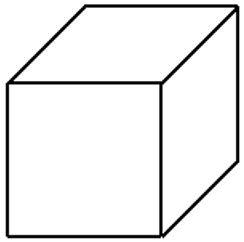
Para comprender mejor las milésimas usaremos una unidad en forma de cubo.
| Tomamos este cubo: | Y ahora lo dividimos en 1000 partes iguales, que llamaremos milésimas: |
 |
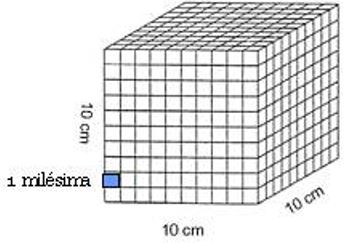 |
Vemos que una unidad puede dividirse en 1000 milésimas. Una milésima es muchísimo menor que una unidad. Esto quiere decir que:
Equivalencias entre décimas, centésimas y milésimas.
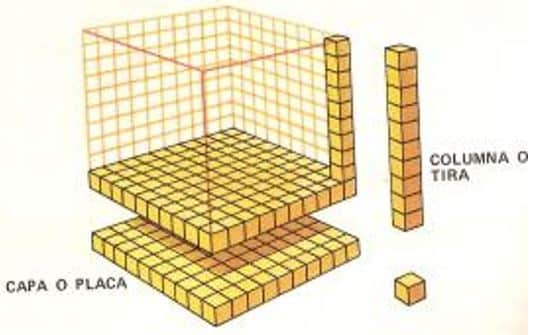
Vamos a ver mejor este cubo para aprender las equivalencias entre décimas, centésimas y milésimas.
| Así se ve el cubo por partes: | En este cubo hay: |
 |
|
Entonces podemos decir que:
- En una capa (décima) hay 10 tiras (centésimas). De manera que 1 décima = 10 centésimas.
- En una capa (décima) hay 100 cubitos (milésimas). Entonces 1 décima = 100 milésimas.
- En una tira (centésima) hay 10 cubitos (milésimas). Por lo que 1 centésima = 10 milésimas.
Ubicación en el cartel de valor de los números decimales
El cartel de valor que hemos conocido desde siempre se amplía con las décimas, las centésimas y las milésimas, que son subórdenes.
Veamos:
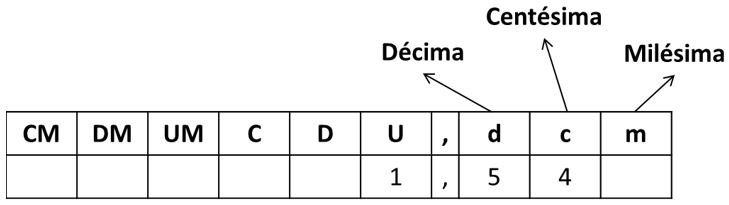
Hemos representado en el cartel de valor el número del ejemplo del principio.
Este número se lee una unidad con cincuenta y cuatro centésimas.
A continuación veremos ejemplos de representación de números decimales en el cartel de valor.
- Ejemplo 1: Cuatro unidades y ciento treinta y seis milésimas

- Ejemplo 2: Dieciséis décimas
Aquí vamos a aplicar las equivalencias que aprendimos antes.
1º Representamos las dieciséis décimas en el suborden correspondiente:
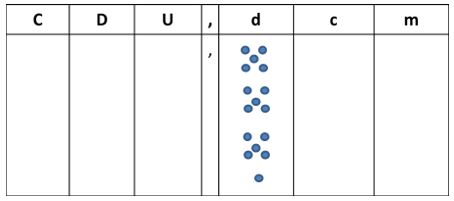
2º Agrupamos 10 décimas para formar una unidad:
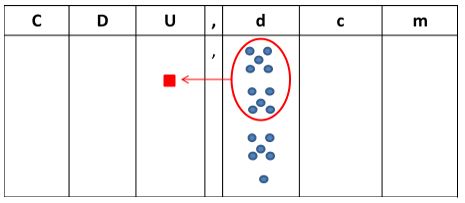
3º Nos queda entonces una unidad y seis décimas:
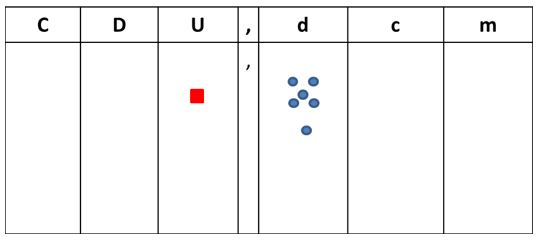
Eso quiere decir que dieciséis décimas las escribimos así en el cartel de valor:
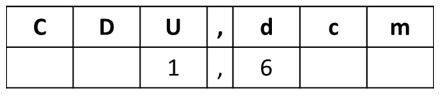
- Ejemplo 3: Veintiuna milésimas
En este caso aplicaremos también las equivalencias que aprendimos.
1º Representamos las veintiuna milésimas en el suborden correspondiente:
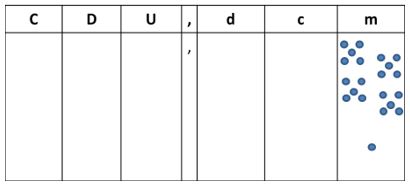
2º Agrupamos 10 milésimas para formar una centésima:
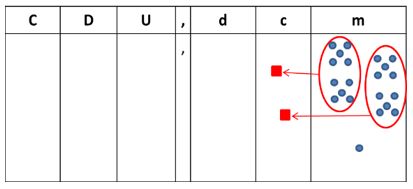
3º Nos queda entonces dos centésimas y una milésima:
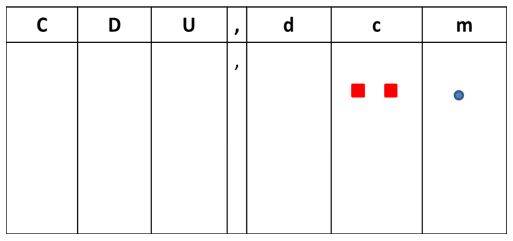
Por eso veintiún milésimas se escribe así en el cartel de valor:
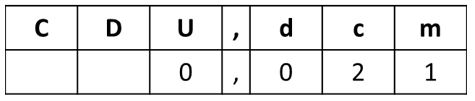
- Más ejemplos:
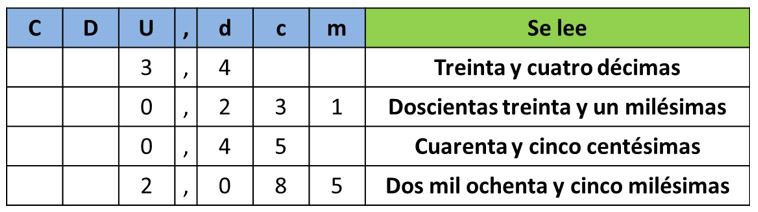
Después de ver la parte decimal de estos números, sus equivalencias y como escribirlos en el cartel de valor, es tu turno para poner en práctica todo ello con esta ficha:
Operaciones con números decimales
En este apartado explicaremos las 4 operaciones básicas con números decimales: adición o suma, sustracción o resta, multiplicación y división.
ADICIÓN O SUMA DE NÚMEROS DECIMALES
La adición de expresiones decimales es muy útil para la vida cotidiana. Cuando vamos de compras, pagamos algunas cuentas o cancelamos los servicios nos vemos en la obligación de hacer alguna adición.
Veamos un ejemplo de dónde y cómo realizar adiciones con expresiones decimales.
Supongamos que una persona quiere comprar los dos productos que aparecen en la imagen y desea saber cuánto le costará adquirirlos.

Entonces, debe sumar el costo de ambos artículos y el total será lo que cancelará.
Para hacer esta operación debes recordar lo que aprendimos anteriormente sobre el cartel de valor.
Esta es la suma que resolveremos:
1,69 + 1,15
Veamos:
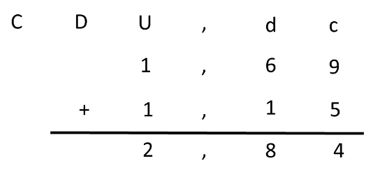
Pero, ¿cómo funciona este algoritmo?
Representamos en el cartel de valor los precios de los productos. Para ello recuerda que cada cifra debe ocupar el orden que le corresponde.
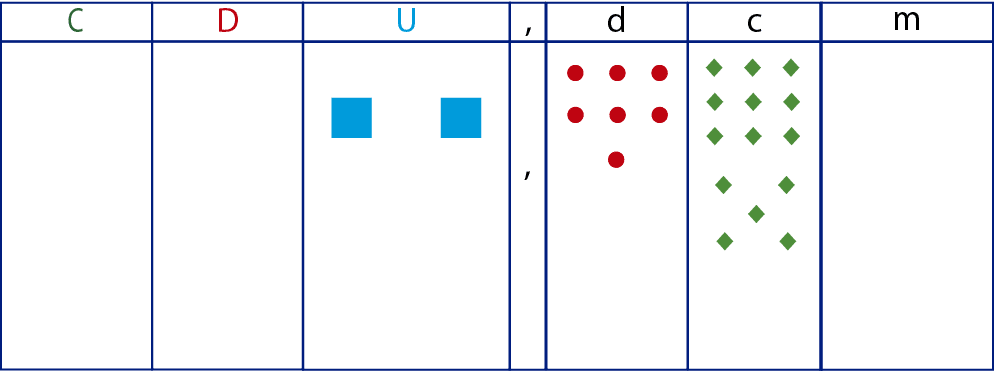
Ahora, agrupamos orden a orden hasta obtener el resultado final.
Como se observa en la imagen, al sumar orden a orden se obtienen 14 centésimas. Por como funciona el sistema de numeración decimal, hicimos un grupo de 10 centésimas que pasaron a formar una décima (10 centésimas = 1 décima).
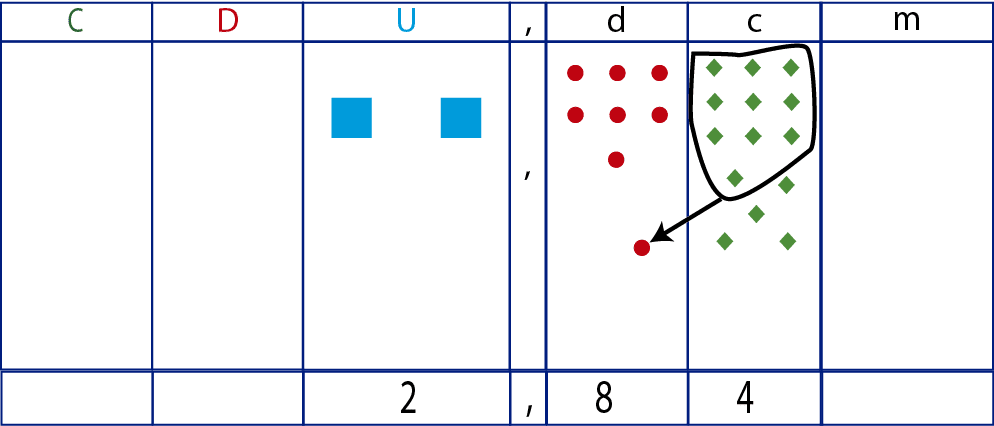
Luego, al hacer la agrupación en el siguiente orden obtenemos siete décimas, incluyendo la que viene de las centésimas.
Por último, al juntar los elementos representados en el orden de las unidades obtenemos dos.
En definitiva, la persona que compre los dos productos debe pagar 2,84 euros.
Hemos visto un ejemplo de cómo hacer adiciones con números decimales, y además hemos contestado a la pregunta de cuánto dinero gastaría la persona que desea comprar los productos de la imagen.
SUSTRACCIÓN O RESTA DE NÚMEROS DECIMALES
Ahora supongamos que para comprar los productos del apartado anterior una persona cuenta con 12,9 euros. Una de las cosas que sería interesante conocer, es cuánto dinero le queda a esta persona luego de pagar 2,84 euros. Veamos:
Esta es la sustracción que resolveremos:
12,9 – 2,84
Veamos:
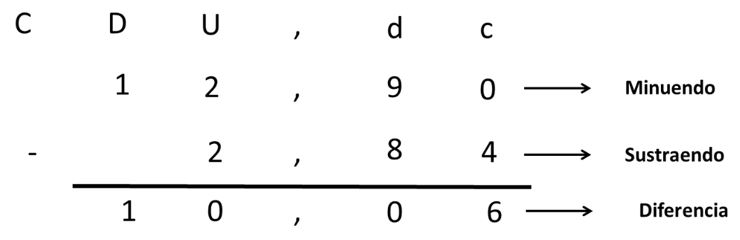
Para ver cómo funciona este algoritmo representaremos la operación en el cartel de valores. Veamos:
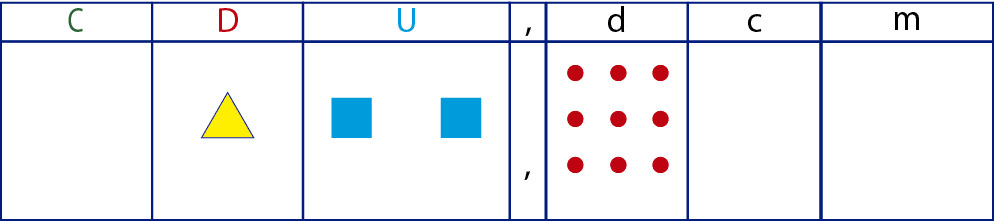
Como se puede observar hemos representado el minuendo de la operación en el cartel de valor. En el siguiente paso quitaremos, orden a orden, del minuendo lo que mande el sustraendo.
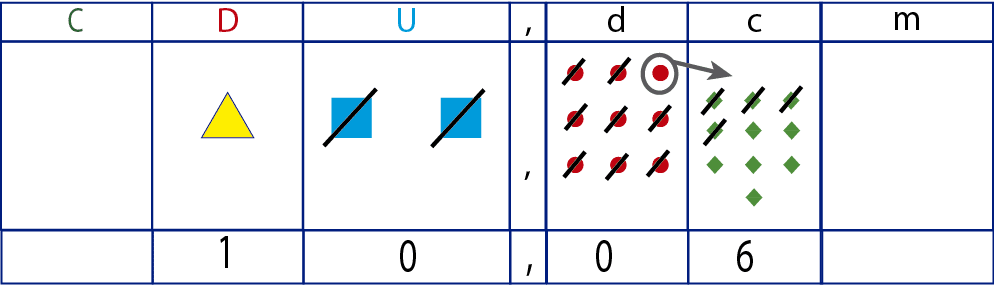
Fíjate que del minuendo debemos quitar 4 centésimas, pero como no había ningún elemento representado en ese orden tuvimos que desagrupar una décima para convertirla en 10 centésimas. Ahora si podemos quitar 4 quedando 6 centésimas.
De las 8 décimas que quedaron en el minuendo, el sustraendo manda a quitar 8, por lo que el resultado es 0 décimas.
Luego quitamos dos unidades del minuendo tal y como lo indica el sustraendo, quedando 0 unidades.
En el orden de las decenas el minuendo queda igual. Entonces, el resultado de restar 12,90 y 2,84 es 10,06.
MULTIPLICACIÓN DE NÚMEROS DECIMALES
La multiplicación de números decimales es una operación que nos permite adicionar (sumar) una misma cantidad, un cierto número de veces.
Por ejemplo, si la multiplicación es 1254,25 x 36, entonces al operar el resultado que se obtiene es equivalente a sumar 36 veces 1254,25.
Los términos de esta multiplicación son:
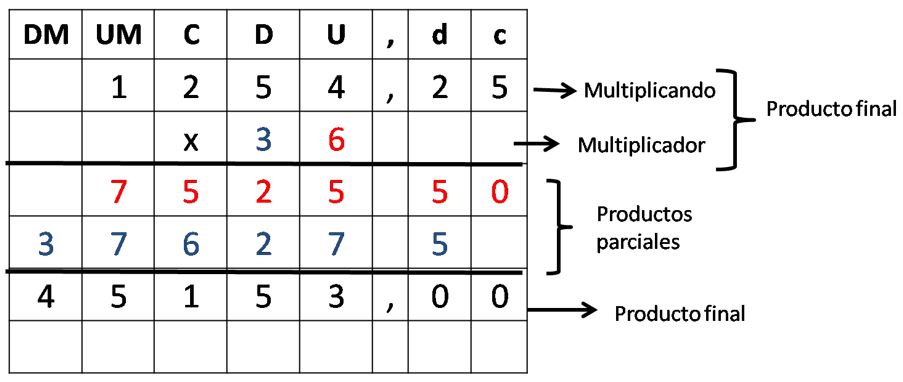
En este caso el multiplicando es un número decimal y el multiplicador un número natural.
Para multiplicar seguiremos el siguiente procedimiento:
- Se comienza la operación multiplicando la cifra que ocupa el lugar de las unidades del multiplicador, en este caso 6, por el multiplicando.

- A continuación se multiplica la decena del multiplicador, en este caso 3, por 1254,25, y el resultado se coloca debajo de 7525,50 dejando un lugar a la derecha. El espacio que se deja a la derecha se debe a que el 3 del multiplicador está ubicado en el orden de las decenas, lo que implica que el producto ya no queda en el orden de las unidades de mil sino en el de las decenas de mil.
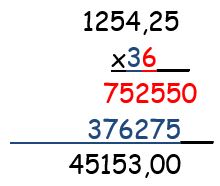
- Por último, se suman los productos parciales para obtener un producto total.
Otro ejemplo de multiplicación de decimales es cuando el multiplicando es un número natural y el multiplicador es una número decimal.
Multiplicaremos 3574 x 4,7. En este caso podemos decir que estamos sumando 3574 veces 4,7 o que estamos sumando 4 veces 3574 más 0,7 veces 3574.
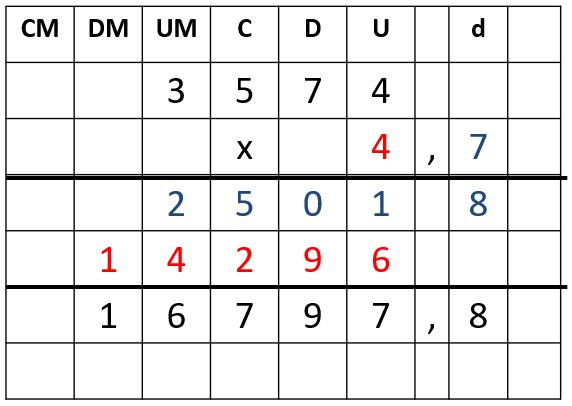
- En este caso se inicia la operación multiplicando la cifra que ocupa el lugar de las décimas en el multiplicador, en este caso 7, por el multiplicando. Es decir:
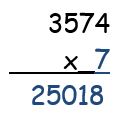
- Seguidamente se multiplica la unidad del multiplicador, en este caso 4, por 3574, y el resultado se coloca debajo de 25018 dejando un lugar a la derecha. El espacio que se deja a la derecha se debe a que al multiplicar 4 x 4 el resultado es 16 unidades y por cómo funciona el sistema de numeración base diez, se copia el 6 en el orden de las unidades y se “lleva 1” al orden de las decenas.

En este último ejemplo trabajaremos con el caso en el que el multiplicando y el multiplicador son números decimales.
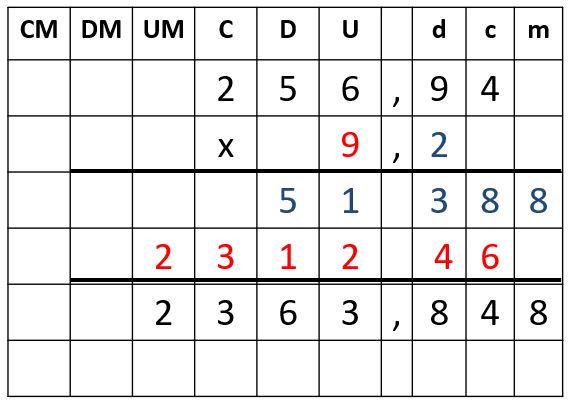
- Se comienza multiplicando la cifra que ocupa el lugar de las décimas en el multiplicador, en este caso 2, por el multiplicando. Es decir:
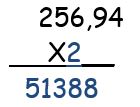
- Seguidamente, se multiplica la cifra de las unidades del multiplicador, en este caso 9, por 256,94, y el resultado se coloca debajo de 51388 dejando un lugar a la derecha. El espacio que se deja a la derecha, se debe a que al multiplicar el 9 ubicado en el orden de la unidades con el 4 representado en el orden de las centésimas, el resultado es 36 centésimas. Con base en el funcionamiento del sistema de numeración decimal, se coloca 6 en el orden de las centésimas y “se llevan 3” al orden décimas.

- Por último, se suman los productos parciales para obtener un producto total.
DIVISIÓN DE NÚMEROS DECIMALES
La división es la operación inversa de la multiplicación. Puede ser exacta si el residuo es cero; o inexacta, si el residuo es distinto de cero.
Fíjate en el ejemplo que se presenta a continuación, allí podrás observar lo que debes hacer para realizar una división:
División de un número decimal entre un natural
En este caso explicaremos paso a paso como funciona el algoritmo de la división. Luego, en los ejemplos siguientes procederemos progresivamente de forma directa.
Primero escribimos la división que vamos a realizar: 974,6 : 8
- Si queremos dividir 974,6 entre 8 nos fijamos en el número del mayor orden. Aquí tenemos 9 centenas, las repartimos entre 8, nos toca a una centena y sobra una.
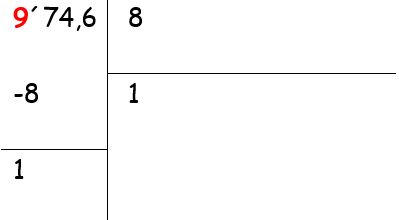
- La centena que sobra son 10 decenas, se las agregamos a las 7 decenas de nuestro número. Esas 17 decenas las repartimos entre 8, tocan a 2 decenas y sobra 1.

- La decena que sobra son 10 unidades, se las agregamos a las 4 unidades de nuestro número y repartimos las 14 unidades entre 8, toca a 1 y sobran 6.
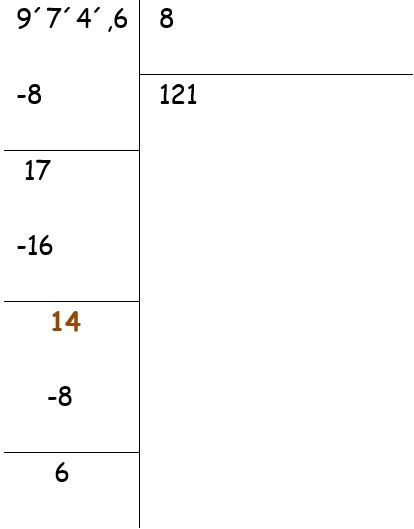
- Las 6 unidades que sobran equivalen a 60 décimas que al sumarlas con las 6 décimas de nuestro número resulta que tenemos 66 décimas que repartidas entre 8 toca a 8 y sobran 2.

El dos del residuo son 2 décimas o también 20 centésimas.
En total obtuvimos que al dividir 974,6 entre 8 el cociente es 121,8 y el residuo son 2 décimas.
Se puede notar que:

División de un número natural entre un decimal
Por ejemplo, dividamos 6782 : 5,6
En este tipo de divisiones lo primero que debemos hacer es transformar el divisor en un número natural. Para ello, haremos lo siguiente:
- Multiplicar el divisor por la unidad seguida de tantos ceros como cifras decimales queramos eliminar (5,6 x 10 =56).
- Multiplicar el dividendo por el mismo número que hayamos multiplicado el divisor (6782 x 10 = 6782).
Realizando estos dos procedimientos obtenemos una división equivalente por lo que el cociente de ambas será el mismo. Es decir, 6782 : 5,6 es equivalente a 67820 : 56.
Realizaremos esta división dejando la resta indicada.
- Vemos que 67 entre 56, es igual a 1. En esta oportunidad multiplicamos 1 por 56 y luego lo restamos de 67 obteniendo como resto parcial 11.
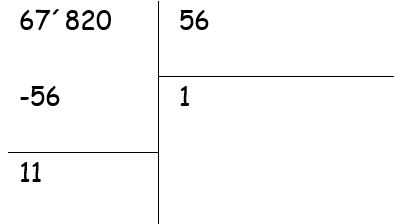
- Ahora bajamos el 8, por lo que dividimos 118 entre 56 que es igual a 2, porque 56 por 2 es 112 y al restarlo de 118 el resto parcial es 6.
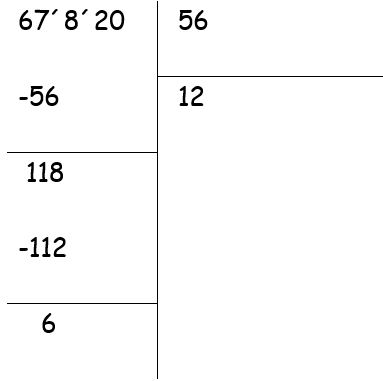
- Nos toca bajar el 2, dividimos 62 entre 56 que es igual 1, porque 56 por 1 es 56 y al restarlo de 62 da un resto de 6.

- Ahora bajamos el 0, por lo que dividimos 60 entre 56 que es igual a 1, porque 56 por 1 es 56 y al restarlo de 60 el resto es 4.
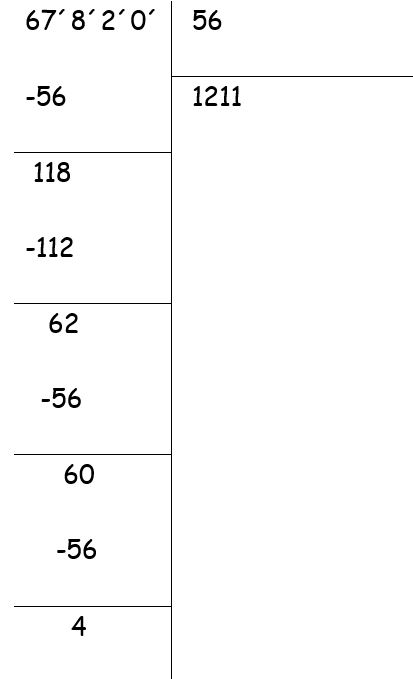
- El cociente de la división 67820 entre 56 es 1211 y el resto 4.
Hay que tener en cuenta que como hemos multiplicado el dividendo y el divisor por un mismo número (el 10 en este ejemplo), el cociente no sufre variaciones, aunque el resto sí, ya que también ha quedado multiplicado por 10. Por tanto hay que dividir 4 entre 10 para obtener el resto de la división original. Es decir, que al dividir 6782 entre 5,6 el cociente es 1211 y el resto es 0,4.
División con números decimales en dividendo y divisor
Vamos a dividir 728,3 entre 5,25.
Nuevamente debemos transformar nuestro divisor en un número natural, para ello aplicamos el mismo procedimiento del ejemplo anterior. En esta oportunidad hay dos decimales en el divisor, por lo que debemos multiplicarlo por (5,25 x 100 = 525) y multiplicar por el mismo número el dividendo (728,3 x 100 = 72830).
De esta manera la división 728,3: 5,25 es equivalente a 72830: 525, después de multiplicar ambos números por 100. En esta oportunidad realizaremos la división de forma directa.

Dividimos 72830: 525.
- 728 entre 525 es igual 1.
- 1 x 5 = 5, al 8 van 3.
- 1 x 2 = 2, al 2 van 0.
- 1 x 5 = 5, al 7 van 2.
- Bajamos el siguiente número que es un 3, por lo que ahora tenemos que dividir 2033 entre 525 que es 3.
- 3 x 5 = 15, al 23 van 8 y nos llevamos 2.
- 3 x 2 = 6 más 2 que nos llevamos son 8, al 13 son 5 y nos llevamos 1.
- 3 x 5 =15 más uno que nos llevamos son 16 al 20 van 4.
- Ahora bajamos el 0 y la división que debemos hacer es 4580 entre 525 que es 8.
- 8 x 5 =40, al 40 van 0 y nos llevamos 4.
- 8 x 2 = 16 más 4 que nos llevamos son 20 al 28 van 8 y nos llevamos 2.
- 89 x 5 = 40 más dos que nos llevamos son 42 al 45 son 3.
- Como ya no hay más cifras que bajar hemos terminado la división.
- Entonces al dividir 72830 : 525 el cociente es 138 y el resto 380.
Como en el ejemplo anterior. El resto que se obtiene ha quedado multiplicado por el mismo número que el divisor, en este caso 100.
Para obtener el resto de la división original (728,3 : 5,25), debemos dividirlo entre 100 (380 : 100 = 3,8). De este modo el cociente de la división 728,3 : 5,25 sigue siendo 138 y el resto es 3,8.
Estrategias de cálculo mental
Calcular mentalmente y con rapidez es una habilidad socialmente muy útil. Los chicos pueden desarrollar esta destreza desde temprana. En este artículo te mostramos algunas estrategias.
Multiplicación por 0,5
- Multiplicar por 0,5 es equivalente a buscar la mitad de uno de los factores. Por ejemplo:
12 x 0,5 = 6
- Con base en lo que hemos visto en uno de los apartados anteriores multiplicar por 12 x 0,5 se puede interpretar como la adición de 12 veces 0,5 que es igual a 6. Este mismo razonamiento aplica para otros casos similares. Veamos:
- 19 x 0,5 = 9,5
- 2,5 x 0,5 = 1,25
- 0,8 x 0,5 = 0,4
- 1,25 x 0,5 = 0,625
Multiplicación por 0,25
- Multiplicar por 0,25 es equivalente a calcular la cuarta parte de uno de los factores de la multiplicación. Por ejemplo:
- 4 x 0,25 = 1
- 12 x 0,25 = 3
- 31 x 0,25 = 7,75
- 1500 x 0,25 = 375
División entre 0,5
- Dividir por 0,5 entre es equivalente a multiplicar por 2. Cuando se divide entre 0,5 se cuentan el número de mitades que hay en el número dado. Veamos:
4 : 0,5 = 8
- Como se observa en la imagen en 4 unidades hay 8mitades por esa razón 4 : 0,5 = 8

- Ejemplos:
- 15 : 0,5 = 30
- 21,5 : 0,5 = 43
- 0,75 : 0,5 = 1,5
- 3,75 : 0,5 = 7,5
Dividir entre 0,25
- Dividir entre 0,25 es equivalente a multiplicar el otro factor de la multiplicación por 4. Es decir:
3 x 0,25 = 12
- Como se puede ver en la imagen en 3 unidades hay 12 cuartas partes. Por esa razón 3 x 0,25 es equivalente a multiplicar 3 x 4.

- Ejemplos:
- 7 : 0,25 = 28
- 10,5 : 0,25 = 42
- 0,5 : 0,25 = 2
- 2,25 : 0,25 = 9
Con las siguientes fichas tendrás la oportunidad de hacer magia, al multiplicar cuando divides y al dividir cuando multiplicas.
Fracciones y números decimales
Como vimos en la primera parte de este artículo, las décimas, centésimas y milésimas se originan al dividir la unidad en 10, 100 y mil partes iguales.
Una décima en fracciones
Recuerda que una décima se obtiene de dividir la unidad en 10 partes iguales.

Al expresar esto en forma de fracción tendríamos lo siguiente:
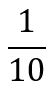
Debemos tener presente que:

Como recordarás, 110 se lee una décima, y ya antes habíamos dicho que 1 décima es igual a 0,1 unidades.
Por tanto, podemos decir que:
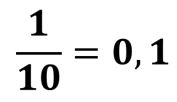
Ambas expresiones se obtienen a partir de dividir 1 unidad en 10 partes iguales.
Una centésima en fracciones
En el caso de la centésima la unidad la habíamos dividido en 100 partes iguales:

Si expresamos esto como una fracción tenemos:
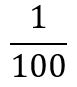
Pues representa 1 de 100 partes iguales en las que dividimos la unidad.
Sabemos también que esta fracción se lee una centésima, y que 1 centésima es igual a 0,01 unidades. Por ello:
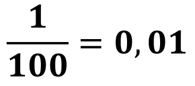
Tanto la expresión decimal como la fracción se obtienen a partir de la división en 100 partes iguales de 1 unidad.
Una milésima en fracciones
Con la milésima tomamos una unidad y la dividimos en 1000 partes iguales:

Al expresarlo en forma de fracción se tiene:
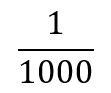
Esto es porque un cubito representa 1 de 1000 partes iguales en las que dividimos la unidad, que en este caso es el cubo entero.
Esta fracción se lee una milésima, y sabemos que 1 milésima es igual a 0,001 unidades. De ahí que:
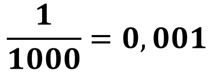
Estas dos expresiones se obtienen de dividir 1 unidad en mil partes iguales.
Ejemplos de fracciones y decimales
- Ejemplo 1: Treinta y cinco décimas
| REPRESENTACIÓN GRÁFICA | REPRESENTACIÓN NUMÉRICA |
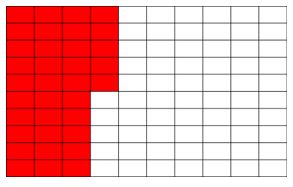 |
Expresado en decimales sería: 0,35 unidades Expresado en fracción es: 35100. |
- Ejemplo 2: Veintitrés décimas
| REPRESENTACIÓN GRÁFICA | REPRESENTACIÓN NUMÉRICA |
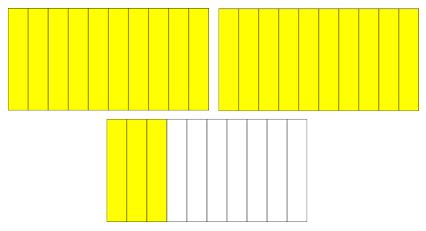 |
Expresado en decimales sería: 2,3 unidades Expresado en fracción es: 2310. |
Cómo convertir números decimales en fracciones
Digamos que quieres convertir el número 0,74 unidades a su expresión en fracciones.
1º Ubicamos el número decimal en el cartel de valor para saber cómo se lee en términos de décimas, centésimas o milésimas.

Vemos que 0,74 representa setenta y cuatro centésimas.
2º Expresamos el denominador con la unidad seguida de ceros dependiendo si es décima (denominador 10), centésima (denominador 100) o milésima (denominador 1000).
En este caso son centésimas por lo que el denominador es 100.
3º Usamos como numerador la cantidad completa sin la coma
En nuestro caso sería:
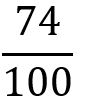
4º Simplificamos la fracción que nos queda. Para ello dividimos numerador y denominador entre un mismo número.
En nuestro ejemplo tenemos:
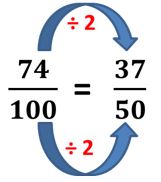
Por último:
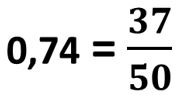
Ejemplos de conversiones de decimales a fracciones:
Veamos esta tabla con cuatro ejemplos de cómo hacer rápidamente este proceso:
| DECIMAL | SE LEE | FRACCIÓN | FRACCIÓN SIMPLIFICADA |
| 1,5 | Quince décimas | 1510 | 32 |
| 2,89 | Doscientas ochenta y nueve centésimas | 289100 | 289100 |
| 3,452 | Tres mil cuatrocientas cincuenta y dos milésimas | 34521000 | 172650 |
| 0,075 | Setenta y cinco milésimas | 751000 | 340 |
Te dejamos unas actividades para practicar:
Selecciona un juego 👇 👇 👇

Números decimales

Ubicar números decimales 1

Ubicar números decimales 2

Ubicar números decimales 3

Suma y resta 1

Sumas y resta 2

Suma y resta 3

Multiplicación 1

Multiplicación 2

Multiplicación 3

División 1

División 2

División 3

División 4

Fracciones y núm. decimales 1

Fracciones y núm. decimales 2

Fracciones y núm. decimales 3

Fracciones y núm. decimales 4

Fracciones y núm. decimales 5

Cuestiionario

Números decimales

Ubicar números decimales 1

Ubicar números decimales 2

Ubicar números decimales 3

Suma y resta 1

Sumas y resta 2

Suma y resta 3

Multiplicación 1

Multiplicación 2

Multiplicación 3

División 1

División 2

División 3

División 4

Fracciones y núm. decimales 1

Fracciones y núm. decimales 2

Fracciones y núm. decimales 3

Fracciones y núm. decimales 4

Fracciones y núm. decimales 5

Cuestiionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.






